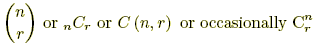Probability
Probability is simply how likely something is to happen.
Whenever we’re unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
Tossing a Coin
When a coin is tossed, there are two possible outcomes:
heads (H) or tails (T)
We say that the probability of the coin landing H is ½ And the probability of the coin landing T is ½.
Throwing Dice
When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6.
The probability of any one of them is 16
Number of ways it can happen
Probability of an event happening = ________________________
Total number of outcomes
Data science often uses statistical inferences to predict or analyze trends from data, while statistical inferences uses probability distributions of data. Hence knowing probability and its applications are important to work effectively on data science problems.
Permutation is the different arrangements of a given number of elements taken one by one, or some, or all at a time. For example, if we have two elements A and B, then there are two possible arrangements, AB and BA. While on the other hand Combination means selection of things. The word selection is used, when the order of things has no importance.The study of permutations and combinations is concerned with determining the number of different ways of arranging and selecting objects out of a given number of objects, without actually listing them. There are some basic counting techniques which will be useful in determining the number of different ways of arranging or selecting objects. The two basic counting principles are given below:
Fundamental principle of counting
Multiplication principle (Fundamental Principle of Counting) Suppose an event E can occur in m different ways and associated with each way of occurring of E, another event F can occur in n different ways, then the total number of occurrence of the two events in the given order is m × n .
Addition principle
If an event E can occur in m ways and another event F can occur in n ways, and suppose that both can not occur together, then E or F can occur in m + n ways.
Number of permutations of ‘n’ different things taken ‘r’ at a time is given by:-
nPr = n!/(n-r)!
The number of possible combination of r objects from a set on n objects.
- KPSC Mains Tests and Notes Program
- KPSC Prelims Exam 2024- Test Series and Notes Program
- KPSC Prelims and Mains Tests Series and Notes Program
- KPSC Detailed Complete Prelims Notes